H ENA production from surfaces

Hydrogen ENA generation from moon surfaces is discussed.

Generation mechanisms

Several mechanisms have been traditionally considered.

• Micrometeorite Viporalization (MV)

• Electron Stimulated Desorption (ESD)

• Photon Stimulated Dissorption (PSD)

• Ion sputtering (ISP)

• Ion back scattering (IBS)

Neutrals from MV is very low temperature (<10000K~1eV). Considering the lower limit of 10 eV for low energy ENA sensors, MV is not considered here. See also [FUTAANA-2006].

ESD and PSD are electric processes, and the typical energy is <10 eV. While for some of the lighter component they might produce amount of neutrals forming exosphere, we do not considere ESD and PSD here by the same reason above. See also [FUTAANA-2006].

The ISP and IBS may produce the ENAs >10 eV, we only consider these two mechanisms.

Ion sputtering

ISP is the mechanism to erode the moon surfaces. A large amount of works have been done since 60s. A famous expression of the sputtered particle distribution is by the [THOMPSON-1968] and modified by [WURZ-2003].

\[F(E) = nC\frac{E}{(E+E_b)^3}\Bigl(1-\sqrt{\frac{E+E_b}{Ei'}}\Bigr)\]

This is the energy distribution. (C is in the unit of “energy”. See equation 1 in WURZ-2007, too, while that is –most probably– normalized.)

Nevertheless, the differential flux is

\[j(E) = F(E) \times v / \Delta\Omega = \sqrt{\frac{2E}{m}}\frac{1}{\Delta\Omega}F(E)\]

Ion backscattering

IBS is the process that the incident particle is reflected back to space. For porous surfaces like Moon, it has been thought that IBS is not dominant source of neutral production, but [WIESER-2009] proved that IBS efficiency is ~20%. According to [FUTAANA-2012] the IBS ENA follows the Maxwell distribution with temperature proportional to velocity.

From a laboratory experiment that we did [REF], the ice surface also reflect back the impinging particles. The reflection rate is calculated preliminarily, and the resulting value is as similar as the case of regolith (~25% in this case). The parametric temperature in the Maxwell form is 2.5–3 times higher than the case of regolith.

Upstream conditions

The production of hydrogen ENA is highly depending on the upstream conditions, i.e. the species and the energy. Table 1 and 2 summarizes the condition used here. Note that the Jupiter environment is not explored well, all the values here specify just one typical value.

Table 1: Upstream condition for Ganymede

Label	Species	Energy	Flux
GCH	Corotational H+	120 eV (cor. flow ~150 km/s)	1.5e7 /cm2 s (cor. density 4 /cm3 * 25%)
GCO	Corotational On+, Sn+	3000 eV (cor. flow ~150 km/s)	4.5e7 /cm2 s (4/cm3 * 75%: Ratio from ES)
GPH	Precip. Cusp H+	2 eV (20 km/s)	2.5e7 /cm2 s (MHD * 25%)
GPO	Precip. Cusp On+, Sn+	50 eV (20 km/s)	7.5e7 /cm2 s (MHD * 75%)
GHH	High energy H+	100 keV (4300 km/s)	5e6 /cm2 s (M04, j(=1e4)*100keV*5sr.)
GHO	High energy On+, Sn+	100 keV (800 km/s)	2e6 /cm2 s (M04, 1/5 of H+, 2 species)

Table 2: Upstream conditions for Europa

Label	Species	Energy	Flux
ECH	Corotational H+	40 eV (cor. flow ~90 km/s)	2.9e8 /cm2 s (cor. density 130/cm3 * 25%)
ECO	Corotational On+, Sn+	1000 eV (cor. flow ~90 km/s)	8.8e8 /cm2 s (130/cm3 * 75%: Ratio from ES)
EHH	High energy H+	100 keV	1.5e7 /cm2 s (P02)
EHO	High energy On+, Sn+	100 keV	1e7 /cm2 s (P02)

ES refers the the Environmental Specification (Issue 4 Rev 9). MHD refers to the MHD results by [JIA-2008]. M04 referes to the [MAUK-2004] (see also Figure 1 in that paper) P02 refers to the [PARANICAU-2002] together with [PLAINAKI-2010]. Otherwise, [KIVELSON-2004] is used.

Note that all the above component is considered to be mono energetic in the following for simplicity. Also note that I did not separate O and S, and the mixed species are assumed to have 25 amu. In the reality, these assumptions are not precise.

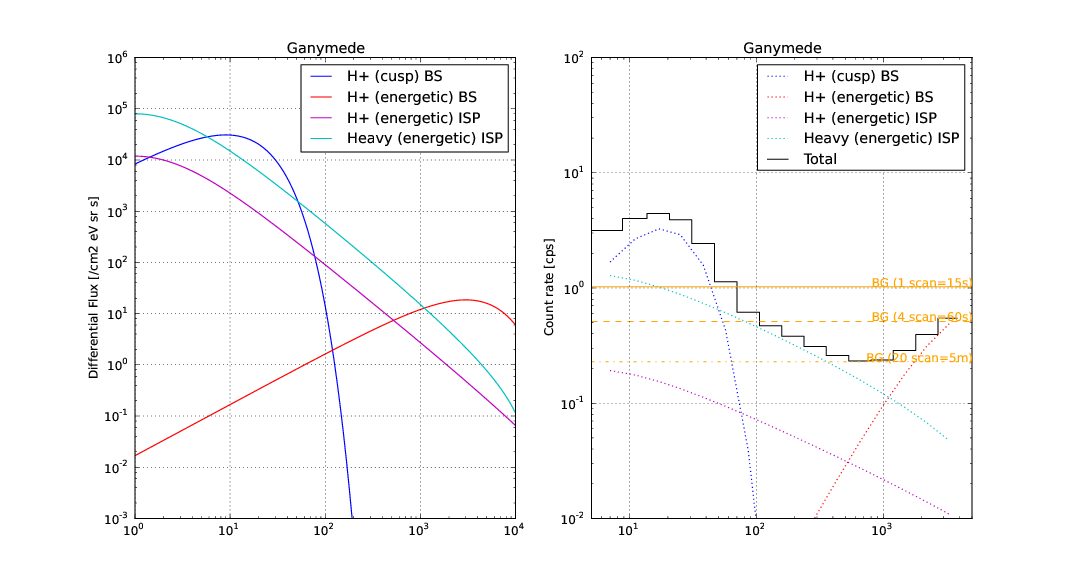
Hydrogen ENA production at Ganymede

Let’s look at the production each by each.

GCH and GPH

For GCH, the 150 km/s flux may produce 33 eV Maxwell distribute H-ENA according to empirical model [FUTAANA-2012]. The temperature may have higher from the ice, due to the different target mass from regolith. From preliminary analysis of ice experiment, the parametric temperature could be higher by a factor of 2-3. The parametric temperature, thus, is taken 80 eV. The reflection rate is assumed to be 25%.

For GPH, the 20 km/s flux might produce 3.5 eV H-ENAs (~9eV considering ice case), but applying the empirical model to this case is rather suspective because of very close energy to the binding energy of the target atoms. Anyway, I applied for somewhat reference purpose.

Sputtering may also contribute for both cases, but not a very high yield is expected from CENA observations. So that I neglected the sputtering yield.

Todo

I have to make energy spectra and count rate plot for this mechanism. Use empirical model.

GHH

For GHH, we do not know the 4300 km/s (100 keV) proton backscattering follows the empirical model, but we do anyway because no reference data.

Nevertheless, the 4300 km/s proton makes 1.2 keV backscattering from empirical model [FUTAANA-2012]. Modification factor of 2.5 is applied to get 3 keV backscattering. Backscattering of 25% rate is kept.

It also sputter H from ice. Not well know process this is (TBC), but I just assume the similar yield of H2O in [SHI-1995], which treats the H2O sputtering by H+. 100 keV H+ can generate yeild 3 for H2O [SHI-1995]. Here I assumed yield of 3.

Todo

Produce the energy spectra and count rate using TS.

Todo

If needed, we should go using 33 keV data in ice experiment. Meanwhile, I would use empirical model for simplicity.

GCS and GPS

First, I just notice that for both case, no backscattering H is generated obviously.

For GCS, the 3 keV heavy ions may sputter hydrogen ENA. We did lab experiment for this energy. However, I just refered to the existing literature survey. From [SHI-1995], the yield is extrapolated to be 3 for 3 keV O+.

For GPS, 50 eV heavy ion also can sputter hydrogen ENA, but we do not have any data. Yield could be very small. So that I ignored.

Todo

I have to make count rate plot for GCS. Use ice11.

GHS

High energy heavy sputters hydrogen a lot. Also according to [SHI-1995], 100 keV O+ will produce H2O with yield 50–60. Here I assumed 50 for H yield.

Todo

Produce the energy spectra and count rate using TS.

For Europa

Europa cases, it is very similar code we can use for Ganymede.

ECH

Corotational plasma has velocity of 90 km/s. The corresponding temperature is 23 eV, and 55 eV after the factor of 2.5 from ice experiment.

ECO

Corotational heavy plasma will produce sputtered H. The energy of the heavy plasma is ~1 keV, the yield is ~1 from [SHI-1995].

EHH

High energy hydrogen makes both backscattering and sputtering.

For backscattering, the same argument to Ganymede case. The temperature would be 3keV for ENAs with .25 fraction.

EHO

High energy oxygen makes sputtering. See Ganymede (GHO).

Results

The results are shown in the following figures.